Exponentialfunktion, Sinus und Cosinus im Komplexen
Definition:
Die Exponentialfunktion
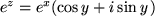 |
Folgerung
Es gilt die Funktionalgleichung
|
Ist
 reell - also y = 0 - so liefert die Definition den üblichen Wert
reell - also y = 0 - so liefert die Definition den üblichen Wert
 der reellen Exponentialfunktion. Die Definition beschreibt also in der Tat eine
Erweiterung der Exponentialfunktion exp ins Komplexe.
der reellen Exponentialfunktion. Die Definition beschreibt also in der Tat eine
Erweiterung der Exponentialfunktion exp ins Komplexe.
Ist
 dagegen imaginär, d.h.
dagegen imaginär, d.h.
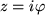 mit
mit
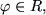 so liefert die Definition:
so liefert die Definition:
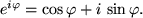
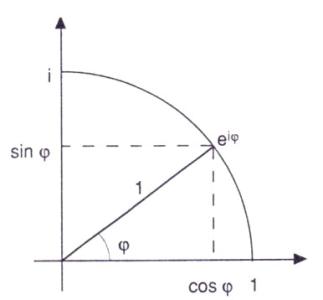
Diese Gleichung lässt sich auf einfache Weise geometrisch deuten:
Der Punkt
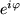 in der komplexen Zahlenebene hat die Komponenten
in der komplexen Zahlenebene hat die Komponenten
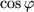 und
und
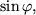 liegt also auf der Einheitskreislinie (siehe Bild).
Dabei bildet die Verbindungsstrecke
liegt also auf der Einheitskreislinie (siehe Bild).
Dabei bildet die Verbindungsstrecke
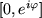 den Winkel
den Winkel
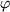 mit der positiven x-Achse.
Läuft
mit der positiven x-Achse.
Läuft
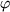 von
von
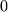 bis
bis
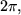 so umrundet
so umrundet
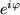 einmal den Einheitskreis im umgekehrten Uhrzeigersinn.
einmal den Einheitskreis im umgekehrten Uhrzeigersinn.
Für
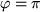 folgt speziell
folgt speziell
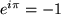 oder
oder
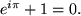
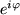 auf der Einheitskreislinie
auf der Einheitskreislinie
Bemerkung
Diese Gleichung wird die schönste Gleichung der Welt genannt,
denn sie verbindet in harmonischer Weise die wichtigsten Zahlen der Analysis:
|
Ersetzt man in der Gleichung
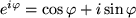
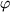 durch
durch
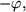 so erhält man
so erhält man
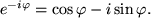
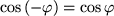 und
und
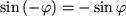 ist.
Wir addieren nun die Gleichungen bzw. subtrahieren sie
und erhalten
ist.
Wir addieren nun die Gleichungen bzw. subtrahieren sie
und erhalten
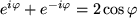
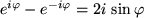
Auflösen nach
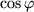 und
und
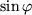 liefert:
liefert:
Folgerung
Für alle reellen Zahlen
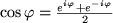 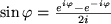 |
Diese Darstellung von Cosinus und Sinus ist für viele Umformungen bequem, da sich mit der Exponentialfunktion sehr bequem rechnen lässt. Man zieht diese Gleichungen überdies zur Definition der trigonometrischen Funktionen im Komplexen heran:
Definition:
Die Sinus- und Cosinus - Funktion sind für beliebige komplexe
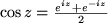 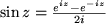 |
Wir bemerken dabei, dass
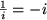 ist, wie man nach Multiplikation der rechten und
der linken Seite mit
ist, wie man nach Multiplikation der rechten und
der linken Seite mit
 sofort sieht.
sofort sieht.
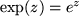 ist für komplexe Zahlen
ist für komplexe Zahlen
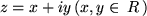 folgendermaßen definiert:
folgendermaßen definiert:
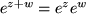 für alle komplexen z, w.
für alle komplexen z, w.
 und
und
 gilt
gilt
 so erklärt:
so erklärt: