Zenons Paradoxon von Achill und der Schildkröte

Der griechische Philosoph Zenon behauptete, der Läufer Achill könne kein Wettrennen gegen eine Schildkröte gewinnen, falls diese vor ihm einen gewissen Vorsprung habe.

Das Rennen war folgendermaßen charakterisiert:

Die Schildkröte bekommt 100 m Vorsprung vor Achill, der aber 10 mal so schnell laufen kann wie die Schildkröte. Hat Achill also die 100 m Vorsprung hinter sich gebracht und ist am Startpunkt der Schildkröte angelangt, so ist diese natürlich auch schon 10 m gelaufen. Achill läuft also auch noch diese 10 m, aber die Schildkröte ist ebenfalls 1 m weitergekommen. Führt man diese Logik fort, so dürfte Achill die Schildkröte niemals erreichen, denn immer wenn er am letzten Aufenthaltspunkt der Schildkröte angelangt ist, ist diese bereits ein Stück vorwärts gekommen ...

__________________

Kann Achill denn die Schildkröte nun tatsächlich nicht einholen??? Und was hat das mit Reihen zu tun???

Schauen wir uns einmal die Einzelstrecken an, die Achill zurücklegt, so ergibt sich die folgende Summe (hier in Metern):

Diese Summe beschreibt eine Reihe und kann explizit so aufgeschrieben werden:

Nun ergibt sich die Frage nach dem Grenzwert dieser Reihe, denn je nachdem, wie dieser aussieht, hat Zenon Recht oder Unrecht. D.h. ist der Grenzwert unendlich, so wird Achill die Schildkröte in der Tat erst nach unendlich vielen Metern einholen. Konvergiert die Reihe dagegen gegen einen bestimmten Wert, so hat sich Zenon geirrt.

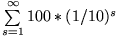
In diesem Beispiel ist es in der Tat so, dass die Reihe gegen einen Grenzwert konvergiert: Die aufzuaddierenden Glieder der Reihe werden immer kleiner und sind spätestens nach dem fünften Glied nicht mehr signifikant, d.h. sie verändern das Ergebnis kaum noch.

Addieren wir nun die ersten fünf Reihenglieder, so ergibt sich folgender Wert (in Meter):

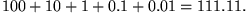
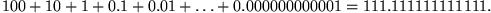
Addieren wir weitere 10 Reihenglieder dazu, so ergibt dies folgenden Wert (in Meter):

Da dieser Wert sich nur minimal von dem ersten ermittelten unterscheidet, wird deutlich, dass bereits sehr früh ein relativ exakter Grenzwert abgeschätzt werden kann.

Zenon hatte also Unrecht mit seiner These. Sein Problem war, dass er von einem unendlich großen Grenzwert ausgegangen ist. Das ist hier, wie gezeigt, nicht der Fall, da die zu addierenden Zahlen immer kleiner werden.

Achill wird also die Schildkröte nach

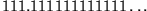
Metern Laufstrecke eingeholt haben!

Bei der hier vorgestellten Reihe handelt es sich um die geometrische Reihe.

Aber Vorsicht: Es gibt Reihen, bei denen die Glieder ebenfalls immer kleiner werden, die aber trotzdem einen unendlich großen Grenzwert haben. Das liegt daran, dass in diesem Fall die Reihenglieder "nicht schnell genug" schrumpfen und daher immer noch in wichtiger Weise zum Endergebnis beitragen.